API Overview ¶

Release:	1.4
Date:	October 13, 2010

This section gives an overview of Bolt’s API. Bolt itself is designed around a number of simple data structures for representing models and input examples. The functionality of Bolt is structured in a number of core modules. Each module provides an abstraction of common functionality. For example there exist modules to represent models, train models, load data sets, or evaluate models.

Contents

API Overview

Data Structures ¶

Bolt itself is constructed around a number of primitive data structures:

Dense vectors

implemented via numpy arrays (numpy.array).
Sparse vectors

implemented via numpy record arrays (numpy.recarray).

Each bolt.model.Model is parametrized by a weight vector which is represented as a 1D numpy.array, allowing efficient random access.

An instance (aka a feature vector), on the other hand, is represented as a s sparse vector via a numpy record array. The data type of the record array is data type bolt.sparsedtype which is a tuple (uint32,float64). The advantage of record arrays is that they are mapped directly to C struct arrays.

The `bolt.model` Module ¶

The bolt.model module contains classes which represent parametric models supported by Bolt.

Currently, the following models are supported:

bolt.model.LinearModel: a linear model for binary classification and regression. bolt.model.GeneralizedLinearModel: a linear model for multi-class classification.

class bolt.model.GeneralizedLinearModel(m, k, biasterm=False)¶

Bases: object

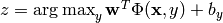A generalized linear model of the form $z = \operatorname*{arg\,max}_y \mathbf{w}^T \Phi(\mathbf{x},y) + b_y$ .

Create a generalized linear model for classification problems with k classes.

Parameters:	m – The dimensionality of the input data (i.e., the number of features). k – The number of classes.

predict(instances, confidence=False)¶

Predicts class of each instances in instances. Optionally, gives confidence score to each prediction if confidence is True. This method yields GeneralizedLinearModel.__call__() for each instance in instances.

Parameters:	confidence – whether to output confidence scores. instances – a sequence of instances.
Returns:	a generator over the class assignments and optionally a confidence score.

probdist(x)¶

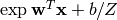The probability distribution of class assignment. Transforms the confidence scores into a probability via a logit function $\exp{\mathbf{w}^T \mathbf{x} + b} / Z$ .

Returns:	a k-dimensional probability vector.

class bolt.model.LinearModel(m, biasterm=False)¶

Bases: object

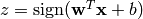A linear model of the form $z = \operatorname{sign}(\mathbf{w}^T \mathbf{x} + b)$ .

Create a linear model with an m-dimensional vector $w = [0,..,0]$ and b = 0.

Parameters:	m (positive integer) – The dimensionality of the classification problem (i.e. the number of features). biasterm (True or False) – Whether or not a bias term (aka offset or intercept) is incorporated.

predict(instances, confidence=False)¶

Evaluates 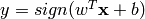$y = sign(w^T \mathbf{x} + b)$ for each instance x in instances. Optionally, gives confidence score to each prediction if confidence is True. This method yields LinearModel.__call__() for each instance in instances.

Parameters:	instances – a sequence of instances. confidence – whether to output confidence scores.
Returns:	a generator over the class assignments and optionally a confidence score.

The `bolt.trainer` Module ¶

The trainer package contains concrete Trainer classes which are used to train a Model on a Dataset.

class bolt.trainer.OVA(trainer)¶

Bases: object

A One-versus-All trainer for multi-class models.

It trains one binary classifier for each class c that predicts the class or all-other classes.

Parameter:	trainer – A concrete Trainer implementation which is used to train k LinearModel classifiers that try to predict one class versus all others.

paralleltrain(glm, dataset, verbose, shuffle, ncpus)¶

serialtrain(glm, dataset, verbose, shuffle)¶

train(glm, dataset, verbose=1, shuffle=False, ncpus=1)¶

Train the glm using k binary LinearModel classifiers by applying the One-versus-All multi-class strategy.

Parameters:	glm – A `bolt.model.GeneralizedLinearModel`. dataset – A Dataset. verbose (int) – Verbose output. shuffle (bool) – Whether to shuffle the training data; argument is passed to OVA.trainer. ncpus (int) – The number of CPUs used for parallel training. If 1 don’t use serialization, if -1 determine automatically.

trainer¶: The concrete trainer for the binary classifiers.

bolt.trainer.paralleltrain_impl(args)¶

The `bolt.trainer.sgd` Module ¶

The bolt.trainer.sgd module is the core of bolt. Its an extension module written in cython containing efficient implementations of Stochastic Gradient Descent and PEGASOS.

The module contains two Trainer classes:

SGD: A plain stochastic gradient descent implementation, supporting various LossFunction and different penalties, including L1, L2, and Elastic-net penalty.

PEGASOS: Similar to SGD, however, after each update it projects the current weight vector onto the L2 ball of radius 1/sqrt(lambda). Currently, only supports hinge loss and L2 penalty.

The module contains a number of concrete LossFunction implementations that can be plugged into the SGD trainer. Bolt provides LossFunctions for Classification and Regression.

The following Classification loss functions are supported:

ModifiedHuber: A quadratical smoothed version of the hinge loss.

Hinge: The loss function employed by the Support Vector Machine classifier.

Log: The loss function of Logistic Regression.

The following Regression loss functions are supported:

SquaredError: Standard squared error loss function.

Huber: Huber robust regression loss.

The module also contains a number of utility function:

predict(): computes the dot product between a sparse and a dense feature vector.

class bolt.trainer.sgd.Classification¶

Bases: bolt.trainer.sgd.LossFunction

Base class for loss functions for classification.

class bolt.trainer.sgd.Hinge¶

Bases: bolt.trainer.sgd.Classification

SVM classification loss for binary classification tasks with y in {-1,1}.

class bolt.trainer.sgd.Huber¶: Bases: bolt.trainer.sgd.Regression

class bolt.trainer.sgd.Log¶

Bases: bolt.trainer.sgd.Classification

Logistic regression loss for binary classification tasks with y in {-1,1}.

class bolt.trainer.sgd.LossFunction¶

Bases: object

Base class for convex loss functions

dloss¶

Evaluate the derivative of the loss function.

Parameters:	p (double) – The prediction. y (double) – The true value.
Returns:	double

loss¶

Evaluate the loss function.

Parameters:	p (double) – The prediction. y (double) – The true value.
Returns:	double

class bolt.trainer.sgd.ModifiedHuber¶

Bases: bolt.trainer.sgd.Classification

Modified Huber loss function for binary classification tasks with y in {-1,1}. Its equivalent to quadratically smoothed SVM with gamma = 2.

See T. Zhang ‘Solving Large Scale Linear Prediction Problems Using Stochastic Gradient Descent’, ICML‘04.

class bolt.trainer.sgd.PEGASOS¶

Bases: object

Primal estimated sub-gradient solver for svm [Shwartz2007].

Parameters:

reg - The regularization parameter lambda (> 0).
epochs - The number of iterations through the dataset.

train¶

Train model on the dataset using PEGASOS.

Parameters:	model – The `LinearModel` that is going to be trained. dataset – The `Dataset`. verbose – The verbosity level. If 0 no output to stdout. shuffle – Whether or not the training data should be shuffled after each epoch.

class bolt.trainer.sgd.Regression¶

Bases: bolt.trainer.sgd.LossFunction

Base class for loss functions for regression.

class bolt.trainer.sgd.SGD¶

Bases: object

Plain stochastic gradient descent solver. The solver supports various LossFunction and different penalties (L1, L2, and Elastic-Net).

References:

SGD implementation inspired by Leon Buttuo’s sgd and [Zhang2004].
L1 penalty via truncation [Tsuruoka2009].
Elastic-net penalty [Zou2005].

Parameters:

loss - The LossFunction.
reg - The regularization parameter lambda.
epochs - The number of iterations through the dataset. Default epochs=5.
norm - Whether to minimize the L1, L2 norm or the Elastic Net (either 1,2, or 3; default 2).
alpha - The elastic net penality parameter (0<=`alpha`<=1). A value of 1 amounts to L2 regularization whereas a value of 0 gives L1 penalty (requires norm=3). Default alpha=0.85.

train¶

Train model on the dataset using SGD.

Parameters:	model – The `bolt.model.LinearModel` that is going to be trained. dataset – The `bolt.io.Dataset`. verbose – The verbosity level. If 0 no output to stdout. shuffle – Whether or not the training data should be shuffled after each epoch.

class bolt.trainer.sgd.SquaredError¶: Bases: bolt.trainer.sgd.Regression

bolt.trainer.sgd.predict()¶

Computes x*w + b efficiently.

Parameters:	x (np.ndarray(dtype=bolt.sparsedtype)) – the instance represented as a sparse vector. w (np.ndarray(dtype=bolt.densedtype)) – the weight vector represented as a dense vector. b (float) – the bias term (aka offset or intercept).
Returns:	A double representing x*w + b.

The `bolt.trainer.avgperceptron` Module ¶

class bolt.trainer.avgperceptron.AveragedPerceptron¶

Bases: object

Averaged Perceptron learning algorithm.

References:

[Freund1998].

Parameters:

epochs - The number of iterations through the dataset. Default epochs=5.

train¶

Train model on the dataset using SGD.

Parameters:	model – The model that is going to be trained. Either `bolt.model.GeneralizedLinearModel` or `bolt.model.LinearModel`. dataset – The `bolt.io.Dataset`. verbose – The verbosity level. If 0 no output to stdout. shuffle – Whether or not the training data should be shuffled after each epoch.

The `bolt.trainer.maxent` Module ¶

class bolt.trainer.maxent.MaxentSGD¶

Bases: object

Stochastic gradient descent solver for maxent (aka multinomial logistic regression). The solver supports various penalties (L1, L2, and Elastic-Net).

References:

SGD implementation inspired by Leon Buttuo’s sgd and [Zhang2004].
L1 penalty via truncation [Tsuruoka2009].
Elastic-net penalty [Zou2005].

Parameters:

reg - The regularization parameter lambda.
epochs - The number of iterations through the dataset. Default epochs=5.
norm - Whether to minimize the L1, L2 norm or the Elastic Net (either 1,2, or 3; default 2).
alpha - The elastic net penality parameter (0<=`alpha`<=1). A value of 1 amounts to L2 regularization whereas a value of 0 gives L1 penalty (requires norm=3). Default alpha=0.85.

train¶

Train model on the dataset using SGD.

Parameters:	model – The `bolt.model.GeneralizedLinearModel` that is going to be trained. dataset – The `bolt.io.Dataset`. verbose – The verbosity level. If 0 no output to stdout. shuffle – Whether or not the training data should be shuffled after each epoch. nprobe – The number of probe examples to determine the learning rate. If -1 use 10 percent of the training data.

The `bolt.io` Module ¶

The bolt.io module provides Dataset specifications and routines for convenient input/output.

The module provides the following classes:

bolt.io.MemoryDataset : an in-memory dataset.

class bolt.io.BinaryDataset(dataset, c)¶

Bases: bolt.io.Dataset

A Dataset wrapper which binarizes the class labels.

Most methods are deligated to the wrapped Dataset. Only BinaryDataset.__iter__() and BinaryDataset.labels() are wrapped.

Creates a binary class wrapper for dataset.

Parameters:	dataset – The Dataset to wrap. c – The positive class. All other classes are treated as negative.

class bolt.io.Dataset¶

Bases: object

Dataset interface.

class bolt.io.MemoryDataset(dim, instances, labels, qids=None)¶

Bases: bolt.io.Dataset

An in-memory dataset. The instances and labels are stored as two parallel arrays. Access to the parallel arrays is via an indexing array which allows convenient shuffeling.

Parameters:

dim (integer) – The dimensionality of the data; the number of features.
instances (numpy.ndarray(dtype=numpy.object)) – An array of instances.
labels (numpy.ndarray(dtype=numpy.float64)) – An array of encoded labels associated with the instances.
qids (numpy.ndarray(dtype=numpy.float64) or None) – An optional array of datatype int32 which holds the query ids of the associated example.

iterinstances()¶: Iterate over instances.

iterlabels()¶: Iterate over labels.

iterqids()¶: Iterate over query ids.

classmethod load(fname, verbose=1, qids=False)¶

Loads the dataset from fname.

Currently, two formats are supported:

numpy binary format
SVM^light format

For binary format the extension of fname has to be .npy, otherwise SVM^light format is assumed. For gzipped files thefilename must end with .gz.

Parameters:	fname – The file name of the seralized `Dataset` verbose (integer) – Verbose output qids (True or False) – Whether to load qids or not
Returns:	The `MemoryDataset`

Examples:

SVM^light format:

>>> ds = bolt.io.MemoryDataset.load('train.txt')

Gzipped SVM^light format:

>>> ds = bolt.io.MemoryDataset.load('train.txt.gz')

Binary format:

>>> ds = bolt.io.MemoryDataset.load('train.npy')

classmethod merge(dsets)¶

Merge a sequence of Dataset objects.

Parameter:	dsets – A list of `MemoryDataset`
Returns:	A `MemoryDataset` containing the merged examples.

sample(nexamples, seed=None)¶

Samples nexamples examples from the dataset.

Parameters:	nexamples (integer) – The number of examples to sample. seed – The random seed.
Returns:	A MemoryDataset containing the nexamples examples.

shuffle(seed=None)¶: Shuffles the index array using numpy.random.shuffle. A seed for the pseudo random number generator can be provided.

split(nfolds)¶

Split the Dataset into nfolds new Dataset objects. The split is done according to the index array. If MemoryDataset.n % nfolds is not 0 the remaining examples are discarded.

Parameter:	nfolds (integer) – The number of folds
Returns:	An array of nfolds MemoryDataset objects; one for each fold

store(fname)¶

Store Dataset in binary form. Uses numpy.save for serialization.

Parameter:	fname – The filename

bolt.io.dense2sparse(x)¶

Convert numpy arrays of bolt.io.densetype to sparse arrays of bolt.io.sparsetype.

Example:

>>> x = np.array([1,0,0,0,0.2], dtype = bolt.io.densedtype)
>>> bolt.dense2sparse(x)
array([(0L, 1.0), (4L, 0.2)], 
  dtype=bolt.io.sparsedtype)

bolt.io.loadDat(filename, qids=False)¶: Load data from svm^light formatted file.

bolt.io.loadNpz(filename, qids=False)¶: Load data from numpy binary format.

bolt.io.sparsedtype¶

The data type of sparse vectors.

Example:

>>> x = np.array([(0,1),(4,0.2)], dtype = sparsedtype)

The `bolt.eval` Module ¶

The eval module contains various routines for model evaluation.

The following evaluation metrics are currently supported:

errorrate(): the error rate of the binary classifier.

rmse(): the root mean squared error of a regressor.

cost(): the cost of a model w.r.t. a given loss function.

bolt.eval.cost(model, ds, loss)¶

The cost of the loss function.

Parameters:	model – A `bolt.model.LinearModel`. ds – A `bolt.io.Dataset`.
Returns:	sum([loss.(model(x),y) for x,y in ds])

bolt.eval.error(model, ds, loss)¶

Report the error of the model on the test examples. If the loss function of the model is bolt.trainer.sgd.Classification then errorrate() is computes, else rmse() is computed if loss function inherits from bolt.trainer.sgd.Regression.

Parameters:	model – A `bolt.model.LinearModel`. ds – A `bolt.io.Dataset`. loss – A `bolt.trainer.sgd.LossFunction`.
Returns:	Either `errorrate()` or `rmse()`; depending on the loss function.

bolt.eval.errorrate(model, ds)¶

Compute the misclassification rate of the model. Assumes that labels are coded as 1 or -1.

zero/one loss: if p*y > 0 then 0 else 1

Parameters:	model – A `bolt.model.LinearModel`. ds – A `bolt.io.Dataset`.
Returns:	(100.0 / n) * sum( p*y > 0 ? 0 : 1 for p,y in ds).

bolt.eval.rmse(model, ds)¶

Compute the root mean squared error of the model.

Parameters:	model – A `bolt.model.LinearModel`. ds – A `bolt.io.Dataset`.
Returns:	sum([(model(x)-y)**2.0 for x,y in ds]).

References ¶

[Shwartz2007]

Shwartz, S. S., Singer, Y., and Srebro, N., Pegasos: Primal estimated sub-gradient solver for svm. In Proceedings of ICML ‘07.

[Tsuruoka2009]

(1, 2) Tsuruoka, Y., Tsujii, J., and Ananiadou, S., Stochastic gradient descent training for l1-regularized log-linear models with cumulative penalty. In Proceedings of the AFNLP/ACL ‘09.

[Zhang2004]

(1, 2) Zhang, T., Solving large scale linear prediction problems using stochastic gradient descent algorithms. In Proceedings of ICML ‘04.

[Zou2005]

(1, 2) Zou, H., and Hastie, T., Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society Series B, 67 (2), 301-320.

[Freund1998]

Freund, Y., and Schapire, R. E., Large margin classification using the perceptron algorithm. In Machine Learning, 37, 277-296.

API Overview ¶

Data Structures ¶

The `bolt.model` Module ¶

The `bolt.trainer` Module ¶

The `bolt.trainer.sgd` Module ¶

The `bolt.trainer.avgperceptron` Module ¶

The `bolt.trainer.maxent` Module ¶

The `bolt.io` Module ¶

The `bolt.eval` Module ¶

References ¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

Previous topic

Next topic

This Page

Quick search

Navigation